Sécurité en ligne – Partie 2 : authenticité d’un message

Cette partie vient compléter celle portant sur le chiffrement asymétrique (Partie 1 – Chapitre 4)

Sommaire

Chapitre 1 : vérifier l'authenticité de la clé publique

Chapitre 2 : vérifier l'authenticité d'un message

Chapitre 1 : vérifier l’authenticité de la clé publique

Objectif : s’assurer que l’on possède bien la véritable clé publique de notre destinataire, que ce n’est pas un usurpateur qui nous a fourni une fausse clé publique pour pouvoir intercepter nos messages.

1.1. Exemple d’une “attaque de l’homme du milieu”

Alice envoie sa clé publique à Betty, mais X l’intercepte, et renvoie à Betty une clé publique dont il détient la clé privée correspondante :

1. Betty chiffre son message avec la clé publique de X, puis envoie son message à Alice.
2. X intercepte le message et le déchiffre pour le lire et éventuellement le modifier. Puis X chiffre à nouveau le message de Betty, avec la véritable clé publique d’Alice, et l’envoie à Alice.
3. Alice déchiffre le message avec sa clé privée, sans se rendre compte de rien. X a usurpé la clé publique de Betty et peut falsifier la signature du message.

Un adversaire peut se positionner en homme du milieu en passant notamment par le fournisseur d’accès internet (tout le trafic obligatoirement passe par lui).

1.2. Solutions

Betty doit vérifier l’authenticité de la clé publique d’Alice. Il existe différents moyens, notamment :

1. Betty peut rencontrer Alice afin de vérifier que la clé publique dont elle dispose est bien la sienne.
2. Betty peut s’appuyer sur une toile de confiance (“web of trust”). Une toile de confiance consiste à établir un lien de confiance de proche en proche. Ainsi, Betty ne connaît pas Alice, mais elle connaît Daniel, qui connaît Émile, qui connaît Alice. Il y a donc un chemin de confiance entre Betty et Alice.

Chapitre 2 : vérifier l’authenticité d’un message

Les paires de clés de chiffrement peuvent aussi être utilisées pour prouver l’authenticité d’un message à l’aide d’une signature numérique.

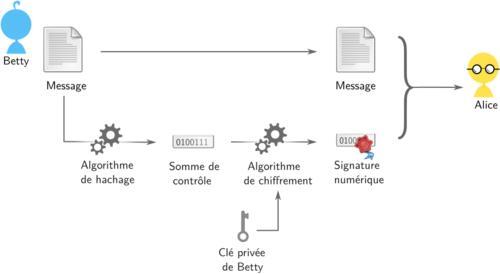
1. Betty veut envoyer un message à Alice, en prouvant qu’elle est bien l’auteure de ce message.
2. L’ordinateur de Betty va dans premier temps calculer la somme de contrôle (empreinte) du message que Betty va envoyer à Alice.
3. Cette empreinte est ensuite chiffrée avec la clé privée de Betty : c’est la signature numérique.
4. Betty envoie son message avec sa signature numérique.
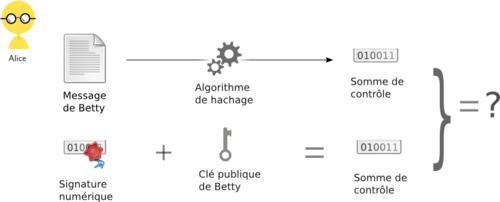
5. Alice réceptionne le message de Betty. L’ordinateur d’Alice calcule à son tour l’empreinte du message, et déchiffre la signature (avec la clé publique de Betty) : si l’empreinte du message calculée est identique à la signature déchiffrée, Alice est certaine de l’authenticité du message reçu.

Betty veut permettre à Alice de vérifier l’authenticité de son message. Elle envoie à Alice un message accompagné de sa signature.

L’ordinateur d’Alice calcule la somme de contrôle du message et déchiffre en parallèle la signature (avec la clé publique de Betty)

Rappel sur le calcul des sommes de contrôle (empreintes)

Pour assurer l’intégrité ou l’authenticité des communications, la cryptographie utilise des outils mathématiques baptisés “fonctions de hachage” : ces fonctions réduisent les objets en petits morceaux appelés somme de contrôle ou empreinte. Une empreinte est généralement écrite sous une forme qui ressemble à ceci :

    f9f5a68a721e3d10baca4d9751bb27f0ac35c7ba

Il suffit alors de comparer les petits morceaux obtenus pour savoir si deux objets sont identiques. Le hachoir fonctionne avec des données de n’importe quelle taille et de n’importe quelle forme : images, CD, logiciels, etc. Il existe plusieurs fonctions de hachage, comme la fonction SHA256 qui n’a pas de défaut connu.